小清水 (@curekoshimizu) です。
本日は FMA についてお話したいと思います。
FMA とは Fused Multiply-Add ことで

の演算のことです。
ここで  は
は  の丸めを表しました。
の丸めを表しました。
本当にただこれだけの内容なのですが、
今回の記事は、この FMA について熱く書いてみたいと思います。
FMA について書くモチベーションなのですが、
本ブログは 精度に関する話題 を多く取り上げてきました。
その中で FMA と関係する話題が非常に多く登場し、
これからも登場予定 です。
そのたびに、
FMA について補足すべきことが多く、
ここでまとめておこうと思い立ちました。
例えばこの記事で FMA 命令と丸め誤差の話がすでに登場しています:
math-koshimizu.hatenablog.jp
この記事を読むと
1. FMA の凄さがわかる
精度や高速化と関わることがわかります。
2. 自分の環境で FMA 命令がサポートしているかがわかる
FMA 命令を積んだ HW の歴史についてある程度まとめてみました。
3. サポートがなくとも無理やり FMA 演算を実行する方法がわかる
FMA 命令を積んでいなくとも FMA 計算する方法がありますので紹介します。
4. コンパイルして FMA 命令を出す方法がわかる
FMA 命令をもっていても、実際に使われなくては意味がありません!
5. FMA の応用がわかる
これと関係して、 Horner 法の起源論文なども載せていたりしますので、
このあたりに興味ある方も是非ご覧ください。
具体的に何がすごいの?
2つのメリットがあります!
1. 丸め回数が減るので精度的に有利
2. HWサポートがある場合に速度的に有利
すごい点その1 – 丸め回数が減るので精度的に有利
上の  を FMA 命令を使わずに計算すると
を FMA 命令を使わずに計算すると

と加算命令1回、乗算命令1回の演算で計算されることになります。
つまり、 2回の丸め が発生します。
それが FMA 命令だと

と 1回の丸めしか入らないため、精度的な観点で有利 になります。
すごい点その2 – HWサポートがある場合に速度的に有利
この FMA は多くの最新 CPU で FMA 命令を HW サポートしています!
さらに CPU だけでなく GPU などの HW でもサポートしていることが多いです。
これにより

という演算を 1回で計算できます。
もっていなければ 乗算命令と加算命令の 2回で 実行する必要があるわけです。
(丸めによる誤差は度外視すると)
これがどういった意味をもつのでしょうか?
この FMA の力をみるべく、
Geforce GTX 1080
という GPU を例に
理論ピーク性能を算出してみましょう。
Geforce GTX 1080 の能力は
で動作し、この CUDA コア1つで 単精度の FMA 命令を発行できます。
FMA は 乗算・加算の 2つの命令分なので 2回の浮動小数点が計算できるという定義になります。
これより 単精度理論ピーク性能 は
2560 (CUDA コア)  1.733 (GHz)
1.733 (GHz)  2 (FLOPS/(CLOCK
2 (FLOPS/(CLOCK  CUDAコア)) = 8872 GFLOPS
CUDAコア)) = 8872 GFLOPS
となります。
FMA 命令をもっていないとこの 「2」 の乗算がなくなりピーク性能指標は、半分になってしまいます。
余談になりますが、この GTX 1080 は単精度で 8.8TFLOPS の力を持っているということで、
2017年現在の GPU はこんなにも能力が高いのか…と思わされます。
このように、
性能指標にも活躍するのが FMA 命令です!
すなわち、
この命令を使わないと事実上、ピーク性能の半分しか理論上だすことができません。
このため、FMA 命令をちゃんと使ってあげることが、
HW の力を引き出しているかどうかと密接な関係があります。
FMA 命令 HW サポートしてる?
ただしこの FMA、
多くの CPU でサポートと書きましたが、
比較的古い CPU を使っている方はサポートされていない可能性 があります。
私の デスクトップ・ノートPC は次のような環境です:
(デスクトップPC)
- CPU : Core i7-3820 CPU @3.60GHz
- メモリ : 64GB (DDR3-1600)
(ノートPC)
- CPU : Core i5-4288U CPU @ 2.60GHz
- メモリ : 8GB (DDR3-1600)
こちら、メモリだけでみると デスクトップの性能がすごくいいです!
しかしながら FMA 命令をサポートしているかどうかでいうと、
ノートPC は FMA命令をサポート しており、デスクトップは 非サポート であります。
そのため、FMA を試す環境としては、私のデスクトップ環境は非常によろしくないです。
このあたりの FMA が載っている載っていないの境界は
2011〜2013 年ごろの CPU にあり、
それについても後述します。
また FMA が載っていなくとも、
FMA の計算、すなわち

の計算をできます!
これは
HW サポートをしていないのでかなり遅いですが、
精度上の恩恵を受けるために使うことができる
という意味です。
これについても 後述 します。
FMA が載っているかどうか怪しいという話を上でしましたが、
何時頃登場したのでしょうか?
最初に FMA 命令を積んだのは 1990年 の IBM RS/6000 です。
IBM RS/6000 に関する論文 「Design of the IBM RISC System/6000 floating-point execution unit」 には次のように書かれています:
The IBM RISC System/6000® (RS/6000) floating-point unit (FPU) exemplifies a second-generation RISC CPU architecture and an implementation which greatly increases floating-point performance and accuracy. The key feature of the FPU is a unified floating-point multiply-add-fused unit (MAF) which performs the accumulate operation (A times B) + C as an indivisible operation.
このように、性能と精度を向上するべく搭載されたのが FMA です。
この当時、この命令は MAD (multiply-add-fused) と略されていたようです。
その後、浮動小数点の規格として採択されたのは 2008 年のことになります。
IEEE754-2008 に FMA について厳格な仕様が定められました。
その仕様が定まる前にも既に
などで実装されていました。
そのため、2008 年頃にはだいたい CPU は FMA 命令もっているのかな?と思います。
歴史的に気をつけたいのが、
我々のデスクトップ環境やノートPCなどで使われている x86_64 、
Intel CPU や AMD CPU です。
対応されたのはまあまあ最近の話 だということがわかります。 (最近の感覚がずれていたらすみません)
これらは Intel CPU であれば Haswell になって、
ようやく FMA サポートしています。
具体的には Intel Core シリーズを最近までの表を下に載せてみますと
- 第1世代: Nehalem
- 第2世代: Sandy Bridge
- 第3世代: Ivy Bridge
- 第4世代: Haswell (2013年頃)
- 第5世代: Broadwell
- 第6世代: Skylake
- 第7世代: Kaby Lake (2017年現在頃)
- 第8世代: Coffee Lake
となっており
第4世代 Haswell から FMA 命令が HWサポートされました。
(デスクトップPC)
- CPU : Core i7-3820 CPU @3.60GHz
- メモリ : 64GB (DDR3-1600)
(ノートPC)
- CPU : Core i5-4288U CPU @ 2.60GHz
- メモリ : 8GB (DDR3-1600)
先ほどの環境の、
「Core i7-3820」 は第2世代 Sandy Bridge (正確には Sandy Bridge-E) であり
FMA 命令をもっていません。
一方でノートPCに載っていた
「Core i5-4288U」 は 第4世代 Haswell のことであります。
一方、
AMD CPU であれば AMD FX、Bulldozer から FMA 命令がサポートされており、
最近の何かと話題な AMD Zen シリーズの Ryzen もサポート済みです。
このあたりは細かいことを言うと、
さらにもう少しややこしく、
レジスタをいくつ使うかという点で異なる FMA3・FMA4 の
どちらを主流とするかの歴史バトルが Intel・AMD でありました。
FMA3 とは例えば


という3レジスタの命令です。一方で FMA4 は

という4レジスタの命令です。
Intel は FMA3 しか最初からサポートしていませんでしたが、
AMD の最初に FMA サポートした Bulldozer (2011年頃) は FMA4 のみをサポートしていました。
最近登場した Ryzen は FMA4 を非サポートとし、 FMA3 のみをサポート としていますから、
FMA3 のほうが主流となりそうです。
さて、上記のような FMA 命令の中のさらに分類の話はおいておくとして、
結局のところ 2011〜2013年付近の x86_64 頃から、大雑把に FMA 命令が使えるようになってきた
ということになります。
(具体的には Intel なら Haswell、AMD ならBulldozer)
ここで誤解しないで頂きたいのは、
Intel 初の FMA 搭載 CPU が Haswell というわけではありません。
例えば、 Itanium という IA-64 が 2001 年頃にありまして、 既に FMA 命令もっていました。
加えて、この年代を超えていたら必ず FMA を持っているというわけではありませんので、
自身の CPU を調べてみてください!
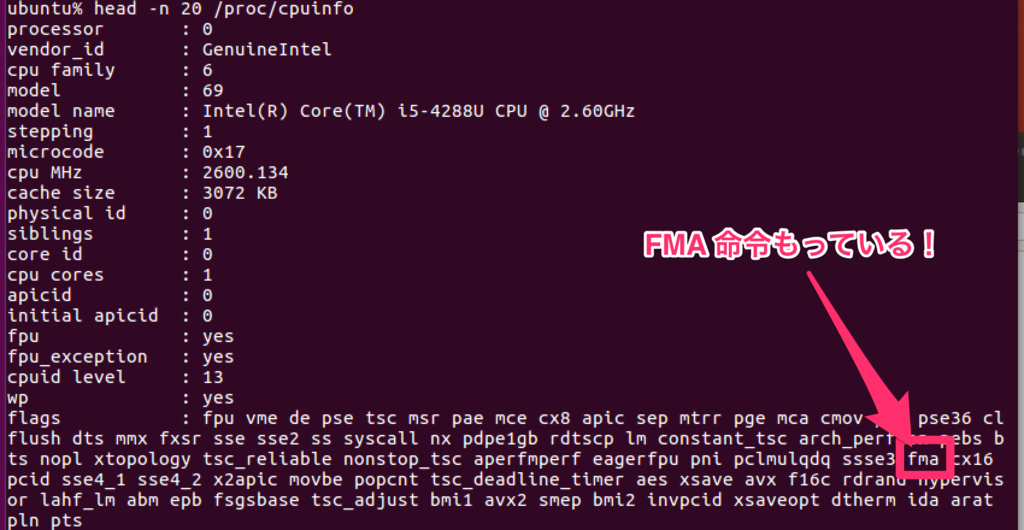
例えば Linux であれば /proc/cpuinfo の中をみてみるとサポートしているかわかります。
(FMAサポートしている:Core i5-4288Uでの結果)
話が脱線気味なので次の話題に移ります。
せっかくFMA命令をもっていても、
実際に使われていなければ意味がありません!
プログラミング言語・コンパイラの最近の状況はどうなのでしょうか?
C言語・C++言語だけの話に限定しますが、
C言語であれば C99 で FMA 計算用の関数をサポートしており、
C++言語であれば C++11 でサポートしています。
具体的には
fmaf・fma・fmal という関数名で提供されています。
順に float・double・long double 用 になります。
C99 は名前の通り1999年の規格なわけですが、
FMA 演算

を HW サポートしていたのは上でも書いたとおり最近の話になります。
実は HW サポートしていなくとも FMA 計算はできます!
ただしかなりの命令数を使うため HWサポートされていない場合は遅いです!!
あまりにも命令数がかかるため、ここでは「FMA計算」とあえて書きました。
ここに注意してください。
例えば FMA を HW サポートしている場合、
コンパイラは自動的に FMA 命令に変更してくれたりするのでしょうか?
実はこのあたりが、さらにややこしい話をもたらします。
このあたり gcc と clang で話が少し違うのです。
gcc も clang も最適化オプションをもっており、
デフォルトでは最適化を行わない設定になっています。
gcc・clnag の最適化オプションとして代表的なものは次です:
- -O0 (default:最適化なし)
- -O1
- -O2
- -O3
- -Ofast
下にいくほどコンパイラにより最適化されます。
参考までに他にも次のような最適化オプションなどがあります:
- -Og : Optimize debugging experience
- -Os : Optimize for size
それぞれの最適化でどういったことをするかについて調査するには、
次を参考にするといいかもしれません:
(gcc)
(clang)
-march=native オプション
上の最適化オプションだけでは CPU による違いは気にしません。
具体的には
先ほどの Intel CPU の
- 第1世代: Nehalem
- 第2世代: Sandy Bridge
- 第3世代: Ivy Bridge
- 第4世代: Haswell (2013年頃)
- 第5世代: Broadwell
- 第6世代: Skylake
- 第7世代: Kaby Lake (2017年現在頃)
- 第8世代: Coffee Lake
といった違いは、
上の -O系のオプションだけをつけても吸収してくれません。
具体的には
上の最適化オプションだけをつけても、
FMA 命令をもつ Haswell と FMA 命令をもたない Sandy Bridge のような CPU のどちらでも
動作できるようにするため、
結論としては 「FMA命令をもたないコード」が生成される ことになります。
高精度・高速度な命令である FMA をもっていても、-O系のオプションをつけるだけでは使われない のです。
非常にもったいないです!
その最適化を支援するために、
この CPU だけでしか使わないよ? とか、 この演算ができるCPUでしか使わないよ? と伝えるオプションがあります。
それが例えば -march=native になります。
例えば gcc 5.4.0 を使って Core i7-3820 が乗った環境では
$ gcc -march=native
をつけるとと次のようなオプションが有効になります:
-march=sandybridge -mmmx -mno-3dnow -msse -msse2 -msse3 -mssse3 -mno-sse4a -mcx16 -msahf -mno-movbe -maes -mno-sha -mpclmul -mpopcnt -mno-abm -mno-lwp -mno-fma -mno-fma4 -mno-xop -mno-bmi -mno-bmi2 -mno-tbm -mavx -mno-avx2 -msse4.2 -msse4.1 -mno-lzcnt -mno-rtm -mno-hle -mno-rdrnd -mno-f16c -mno-fsgsbase -mno-rdseed -mno-prfchw -mno-adx -mfxsr -mxsave -mxsaveopt -mno-avx512f -mno-avx512er -mno-avx512cd -mno-avx512pf -mno-prefetchwt1 -mno-clflushopt -mno-xsavec -mno-xsaves -mno-avx512dq -mno-avx512bw -mno-avx512vl -mno-avx512ifma -mno-avx512vbmi -mno-clwb -mno-pcommit -mno-mwaitx --param l1-cache-size=32 --param l1-cache-line-size=64 --param l2-cache-size=10240 -mtune=sandybridge
例えば キャッシュの大きさや SSE命令 (Streaming SIMD Extensions) のどれをサポートしているかなどを、
コンパイラに伝えていることがわかります。
ここでわかることは、
-mno-fma
-mno-fma4
-avx512ifma
というオプションがついており、FMA命令をもっていないんだろうな…
ということが容易に想像つきます。
-march=native でどういったオプションが有効になるかについては次の記事が参考になります:
また、ここまで紹介した -O1/-O2/-O3/-Ofast や -march=native をつけるとどの程度速くなるかについては、
例えば次の記事が参考になるかもしれません:
http://www.phoronix.com/scan.php?page=news_item&px=GCC-Optimizations-E3V5-Levels
このあたりの最適化オプションを勉強するだけでも面白いです。
FMA が発行されるための最適化オプションは?
FMA 命令をもった Haswell 環境で次のコードをコンパイルしてみましょう。
float fma_test(float x, float y, float z)
{
return x*y + z;
}
$ gcc -S hoge.c
でコンパイルすると次のようになります:
.....
mulsd -16(%rbp), xmm0
addsd -24(%rbp), %xmm0
.....
つまりは FMA命令が使われず乗算と加算命令 で実行されることになります。
$ gcc -O3 -march=native
でコンパイルするとどうでしょうか?
.....
vfmadd132sd %xmm1, %xmm2, %xmm0
.....
と FMA 命令 (詳しくは上で説明したFMA3命令) が発行されていることがわかります。
一方で
$ clang -O3 -march=native
はどうでしょうか?
.....
vmulsd %xmm1, %xmm0, %xmm0
vaddsd %xmm2, %xmm0, %xmm0
.....
と FMA 命令が使われません。
つまり、気をつけたいポイントは
gcc・clang のオプションを揃えても FMA 化されるか違う場合がある
ということです。
この違いを調査した表が次になります:
float fma_test(float x, float y, float z)
{
return x*y + z;
}
上のコードは次のオプションで FMA命令 が呼ばれるかの表
(Core i5-4288U CPU (Haswell/ FMA をもつCPU))
| オプション |
gcc 5.4.0 |
clang 3.8.0 |
| -O0 |
× |
× |
| -O1 |
× |
× |
| -O2 |
× |
× |
| -O3 |
× |
× |
| -Ofast |
× |
× |
| -march=native -O0 |
× |
× |
| -march=native -O1 |
× |
× |
| -march=native -O2 |
○ |
× |
| -march=native -O3 |
○ |
× |
| -march=native -Ofast |
○ |
○ |
(Core i7-3820 (Haswell/ FMA をもたないCPU))
| オプション |
gcc 5.4.0 |
clang 3.8.0 |
| -O0 |
× |
× |
| -O1 |
× |
× |
| -O2 |
× |
× |
| -O3 |
× |
× |
| -Ofast |
× |
× |
| -march=native -O0 |
× |
× |
| -march=native -O1 |
× |
× |
| -march=native -O2 |
× |
× |
| -march=native -O3 |
× |
× |
| -march=native -Ofast |
× |
× |
まず march=native の重要性がわかります。 これがないと FMA 命令をもたないかもしれませんので FMA 命令は発行されません。
また gcc と clang で FMA が有効になる最適化ポイントが違います。
gcc ならば -O2 から clang なら -Ofast から のようです。
-ffp-contract というオプションがあるのですが、
これをつけると clang でも -O1 から可能ならば fma 命令が発行されるようになります。
| オプション |
gcc 5.4.0 |
clang 3.8.0 |
| -ffp-contract=fast -march=native -O0 |
× |
× |
| -ffp-contract=fast -march=native -O1 |
× |
○(変更点) |
| -ffp-contract=fast -march=native -O2 |
○ |
○(変更点) |
| -ffp-contract=fast -march=native -O3 |
○ |
○(変更点) |
| -ffp-contract=fast -march=native -Ofast |
○ |
○ |
この -ffp-contract は gcc のリファレンスにこのように記載されています:
-ffp-contract=off disables floating-point expression contraction. -ffp-contract=fast enables floating-point expression contraction such as forming of fused multiply-add operations if the target has native support for them. -ffp-contract=on enables floating-point expression contraction if allowed by the language standard. This is currently not implemented and treated equal to -ffp-contract=off.
The default is -ffp-contract=fast.
これをみると gcc は既に -ffp-contract オプションがついています。
一方で clang は挙動が変わったことからもデフォルトが fast になっていないようです。
このあたりに コンパイラの思想の違いがある ように見受けられます。
また、 gcc でも -O1 で最適化してもらうには
-fexpensive-optimizations をつけると大丈夫です。
さらに、 -march=native は
いくつかのオプションをつけてもらうためのものだったわけですが、
実際のところは -mfma が本質的です。
そのためまとめると
float fma_test(float x, float y, float z)
{
return x*y + z;
}
というコードは
$ gcc -march=native -O2
$ gcc -march=native -O1 -fexpensive-optimizations
$ gcc -mfma -O2
$ gcc -mfma -O1 -fexpensive-optimizations
$ clang -march=native -Ofast
$ clang -march=native -O1 -ffp-contract=fast
$ clang -mfma -Ofast
$ clang -mfma -O1 -ffp-contract=fast
のいずれかで FMA 命令に展開されることがわかります。
#include <math.h>
float fma_test(float x, float y, float z)
{
return fma(x, y, z);
}
としてみましょう。
この場合は
(Core i5-4288U CPU (Haswell/ FMA をもつCPU))
| オプション |
gcc 5.4.0 |
clang 3.8.0 |
| -O0 |
× |
× |
| -O1 |
× |
× |
| -O2 |
× |
× |
| -O3 |
× |
× |
| -Ofast |
× |
× |
| -march=native -O0 |
○ |
○ |
| -march=native -O1 |
○ |
○ |
| -march=native -O2 |
○ |
○ |
| -march=native -O3 |
○ |
○ |
| -march=native -Ofast |
○ |
○ |
(Core i7-3820 (Haswell/ FMA をもたないCPU))
| オプション |
gcc 5.4.0 |
clang 3.8.0 |
| -O0 |
× |
× |
| …. |
…. |
…. |
| -march=native -Ofast |
× |
× |
となり、HW命令さえもっていれば FMA に展開されます。
そのため、どうしても FMA を発行させたい場合には有効な方法と言えます。
まとめますと
#include <math.h>
float fma_test(float x, float y, float z)
{
return fma(x, y, z);
}
というコードは
$ gcc -march=native
$ gcc -mfma
$ clang -march=native
$ clang -mfma
で展開されます。こちらは -O0 でも大丈夫なところが大きな違いです。
また、 clang であっても -ffp-contract=fast も必要ありません。
それは既にユーザーが FMA 演算箇所を指定しているからです。
FMA の ハードウェアサポートがない場合に C99 FMA 関数 を呼ぶと?
この計算が

きちんと発行できます!
ただし、問題は
複数命令で実行しているので遅い という点です。
それをみるべく次のことをみてみましょう。
HWサポートがない場合に
単精度浮動小数点用の C99 FMA 関数の fmaf を使った実行ファイルを nm コマンドにかけてみますと
$ nm a.out | grep fmaf
U fmaf@@GLIBC_2.2.5
となり glibc の fmaf 関数を呼んでいる ことがわかります。
具体的には glibc のコードの
sysdeps/ieee754/dbl-64/s_fmaf.c
が呼ばれており、ソフトウェアで実装されています。
この実装は次の論文が元になっています:
つまり、高速化という観点ではなく丸めの影響を抑えるため、
複数の計算で実現しているというわけです。
これについては丸め誤差の面白い技法が使われており、
詳しく紹介してみたいと思っております。
ここまでいろいろ知らないと、 FMA 命令の恩恵が得られないことがわかります。
そして、FMA 命令を使うことなんてそんなにあるの? という声があります。
非常にたくさんあります!
紹介する事例が多すぎるため、
ここでは 多項式計算 で考えてみたいと思います。
次の多項式を考えてみましょう

こうした例えば 5次の方程式を計算することがあると思いますが、
 という式を
という式を  回の乗算 で計算すると
0+1+2+3+4+5+6+7 = 28回の乗算と 7回の加減算で実行することになります。
つまり 35 回の丸めが発生します。
回の乗算 で計算すると
0+1+2+3+4+5+6+7 = 28回の乗算と 7回の加減算で実行することになります。
つまり 35 回の丸めが発生します。
これを例えば次のような括弧の付け方で考えます

すると、
 という式を
という式を  回の乗算 で計算すると
0+0+1+2+3+4+5+6 = 21回の乗算と 7回のFMAで実行することになります。
つまり 28 回の丸めが発生します。
回の乗算 で計算すると
0+0+1+2+3+4+5+6 = 21回の乗算と 7回のFMAで実行することになります。
つまり 28 回の丸めが発生します。
つまり 35 回の丸めが入る式から 28 回の丸めが入る式 に変わりました。
さらに、上の 5次方程式は次の Horner 法とよばれる形に変換してあげることができます:

こうすると FMA 7 回で計算できてしまいます。
ちなみに Honer法 (ホーナー法) は非常に有名であり、
気になり起源論文も調べてみました。
1819年の Honer の論文になります:
もちろんこの Honer法 は有名なのですが、
高速化の観点にたてば、例えばこのような式変形も注目すべきです。

この方法にしますと
7回の FMA 演算で計算できてしまいます。
この特徴は 並列に計算可能 な 4つの FMA 演算が
登場することであり、この点で Honer 法より有利に働きます。
こうした多項式計算技法はいろいろ知られており、どこかでまとめたいと思っています。
最後に
ここまで FMA についていろいろ紹介してみました。
FMA はかなり役に立つ命令だったり、
性能向上に役立つものですので、
是非ご活用ください!
また、もし家庭でPCの購入予算がおりない場合、
今のPCはFMAがサポートしてないけど最近のはFMAが載っているから、
だいたい2倍くらい性能いいらしいよ!っていえば
奥さんも説得できそうな気がします。
そんな時にも使ってみてください。
FMA は丸め誤差の話とすごく関わるため、今後このブログでは頻繁に登場予定です!
よろしくお願いします。
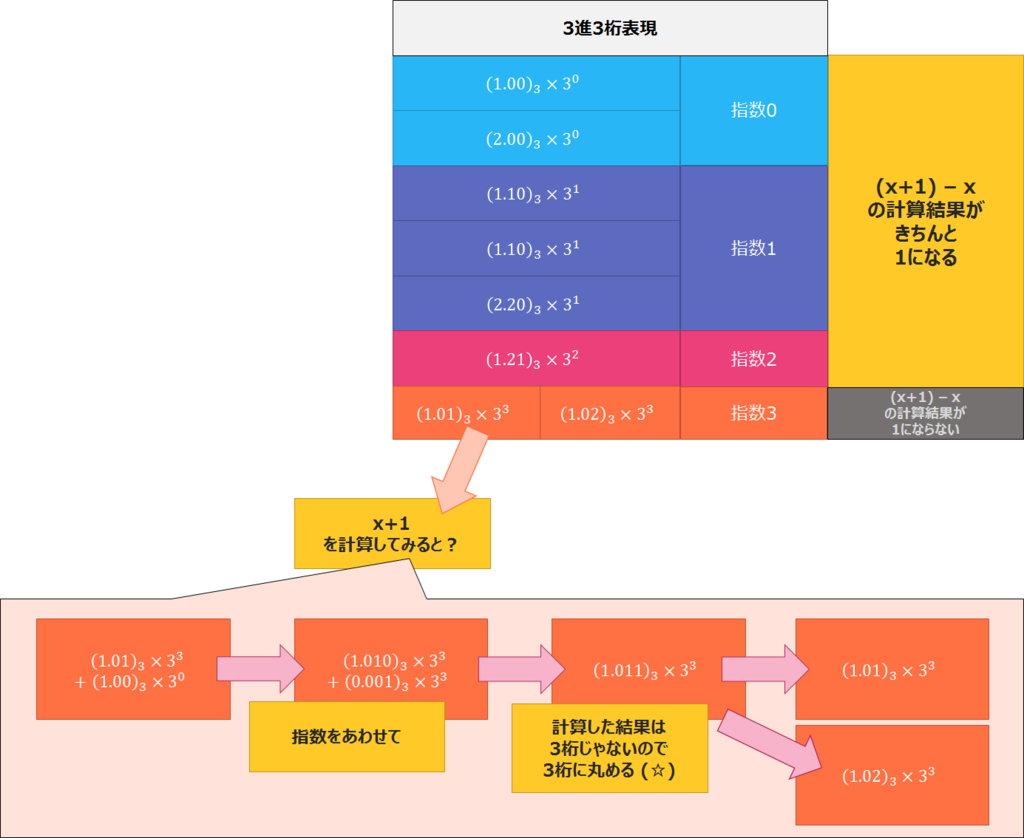
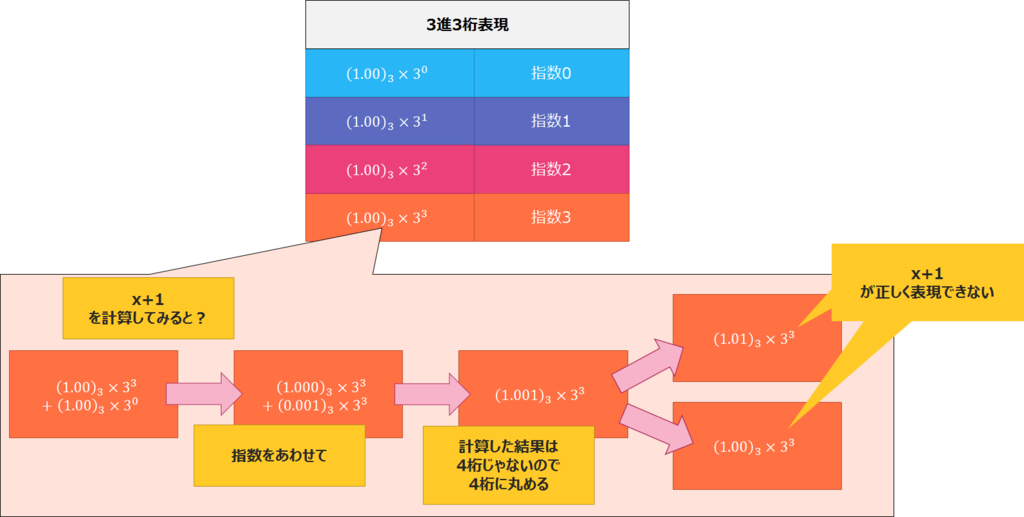
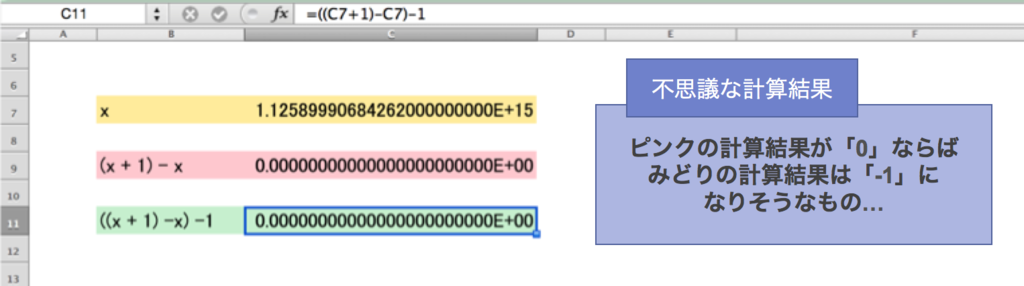
こんなにも数式が出てこなかったのは、この記事が初めてかもしれません。
から計算して、
としてはいけないというお話になります。
の計算ができます。
を計算できます。