小清水 (@curekoshimizu) です。

計算ツールに対して

その計算精度がわかると便利ではないでしょうか？

例えば、コンピュータにのっている

その Excel はどのくらいの精度で計算してくれる？

こうしたアプリケーションだけでなく、

そのコンピュータの中に入っている、

Intel の CPU はどのくらいの精度で計算してくれる？

こういうことがわかると 非常に便利・ワクワク します！

特に CPU にはいろんな精度で計算できる命令が揃っており、

Intel x86_64 CPU ですと

単精度
倍精度
拡張倍精度

の命令が載っています。

この記事を読むと、

実感をもってこれらの精度がわかってしまいます。

f:id:curekoshimizu:20170106231338p:plain

しかも数学的背景もあるので納得もできます！

Abstract

1. CPU 単精度・倍精度の計算精度を当てる

2. CPU 拡張倍精度の計算精度を当てる

3. Excel の計算精度を当てる!?

こういう話のとき Excel の例を最初に書きそうなものです。

なぜだか Excel の例が最後になっていますが

それは困った話が見つかってしまったからです。

1. CPU 単精度・倍精度の計算精度を当てる

プログラミングを勉強すると必ず習う計算環境である、

単精度・倍精度の浮動小数点環境の計算精度をまとめてみましょう。

単精度の浮動小数点 (float・binary32) 環境は 2進24桁精度

倍精度の浮動小数点 (double・binary64) 環境は 2進53桁精度

と言われています。これを実証してみましょう

精度を確かめるプログラムの方針

((x + 1) - x) と 1 が同じ

となるのが、

普通の実数の世界 であります。

当たり前です。

しかしながら、

普通じゃないのが 浮動小数点数 であり、

この2つの式が成立しない場合があります。

Step1

${x}_{p} = {2}^{p}$ の形で

$p = 0$ から初めて大きくしていき

初めて成立しなくなる $p$ を見つけます

Step2

その $p$ の ${x}_{p} = {2}^{p}$ に対して

$(( x_p + 1) - x_p) \neq 1$

が成立しています。

この 1 を動かして

$(( x_p + 2) - x_p) \neq 2$

$(( x_p + 3) - x_p) \neq 3$

と続き、

初めて等号となってしまう整数 $\beta$ を見つけます

つまり、

$(( x_p + \beta) - x_p) = \beta$

となる $\beta$ です。

この $\beta$ がわかると

$\beta$ 進数計算環境であることがわかる

Step3

Step2 でわかった $\beta$ を使って

もう一度 Step1 に似たアルゴリズムを実施します。

${y}_{p} = {\beta}^{p}$ の形で

$p = 0$ から初めて大きくしていき

初めて成立しなくなる $p$ を見つけます

つまり $(( y_p + 1) - y_p) \neq 1$ となる

初めての $p$ が精度 $p$ 桁を表す

という主張です。

補足的には、

2進数であることがわかっていればStep1とStep3 は等価になります。

このことについて

証明は次回の記事とさせていただき、計算例を見てみましょう

実際のプログラム

#include <stdio.h>

void check_float_precision(void)
{
    /* Step. 1 */
    float xp;
    for (xp = 1.0f; (xp + 1.0f) - xp == 1.0f; xp *= 2.0f) ;

    /* Step. 2 */
    float beta;
    for (beta = 1.0f ; (xp + beta) - xp != beta; beta += 1.0f) ;
    printf("base : %d\n", (int)beta);

    /* Step. 3 */
    int precision = 0;
    for (xp = 1.0f; (xp + 1.0f) - xp == 1.0f; xp *= beta) {
        precision++;
    }
    printf("precision : %d\n", precision);
}

void check_double_precision(void)
{
    /* Step. 1 */
    double xp;
    for (xp = 1.0; (xp + 1.0) - xp == 1.0f; xp *= 2.0) ;

    /* Step. 2 */
    double beta;
    for (beta = 1.0 ; (xp + beta) - xp != beta; beta += 1.0) ;
    printf("base : %d\n", (int)beta);

    /* Step. 3 */
    int precision = 0;
    for (xp = 1.0; (xp + 1.0) - xp == 1.0; xp *= beta) {
        precision++;
    }
    printf("precision : %d\n", precision);
}

int main(void)
{
    check_float_precision();
    check_double_precision();

    return 0;
}

実行結果

base : 2
precision : 24
base : 2
precision : 53

と先程紹介したとおり、

2進24桁・2進53桁精度 の「2・24・2・53」が出力されております。

さらに次の例をみてみましょう。

2. CPU 拡張倍精度の計算精度を当てる

CPU は過去互換性を大事にしており、

Intel x86_64 CPU にはすごく昔によく用いられていた、

x87 命令といわれている、

拡張倍精度命令 というものをもっております。

拡張倍精度環境は 2進64桁精度 と言われています。

こうした 古めかしい命令 もわかってしまうのでしょうか？

gcc を使ったコンパイルで -mfpmath=387 オプションをつけると、

強制してこの x87命令で計算することができます。

$ gcc -mfpmath=387 precision_check.c -o precision_check
$ ./precision_check

実行結果

base : 2
precision : 64
base : 2
precision : 64

float・double と宣言したプログラムであっても、

それが　無視されて 先程紹介したとおり、

2進64桁精度 の「64」が出力されております。

3. Excel の計算精度を当てる!?

先程のアルゴリズムを Excel でも計算してみましょう。

B列に $x_p = {2}^{p}$ を計算し、

その結果を使い $(x_p + n) - x_p$ を計算した表を作成します。

この表を使えば

f:id:curekoshimizu:20170122141737p:plain

となり、

f:id:curekoshimizu:20170122141743p:plain

このことから

Excelは 2進50桁の計算環境であることがわかります。

と思いますよね？

2進50桁ってなんだ？ということになるわけです。

なぜならあまり聞き慣れない精度のためです。

よく使われる精度は上でこれまででてきた

2進24桁 (単精度)
2進53桁 (倍精度)
2進64桁 (拡張倍精度)

であります。

ためしに、上の表を次のように変えてみます。

$(x_p + n) - x_p$ を計算するのではなく

$((x_p + n) - x_p) - n$ を計算してみます。

そして、正しく計算されたところは 0 になります。

f:id:curekoshimizu:20170122142854p:plain

もっと下まで計算しますと

f:id:curekoshimizu:20170122142859p:plain

となり、

同じく2進数であることは確かめられるのですが、

Excelは 2進53桁の計算環境になりました。

何がいいたい？

ある方法だと Excel は「2進50桁」

ある方法だと Excel は「2進53桁」(倍精度) という結果になりました。

どうしてこうなったのかわからないため、

Excel詳しい方教えてください！

ちなみにですが CPU の倍精度環境で同じ計算をすると、

$((x_p + n) - x_p) - n$ の表と同じ結果を得ますので、

Excel はおそらく倍精度精度で計算できるのだと思いますが…。

ということはアルゴリズムがおかしい？

このアルゴリズムは浮動小数点環境の精度を求める方法として

よく知られたはずの方法なのですが

端的にいうと Excel の次のおかしな結果のせいで求められないことがわかります：

f:id:curekoshimizu:20170122150814p:plain

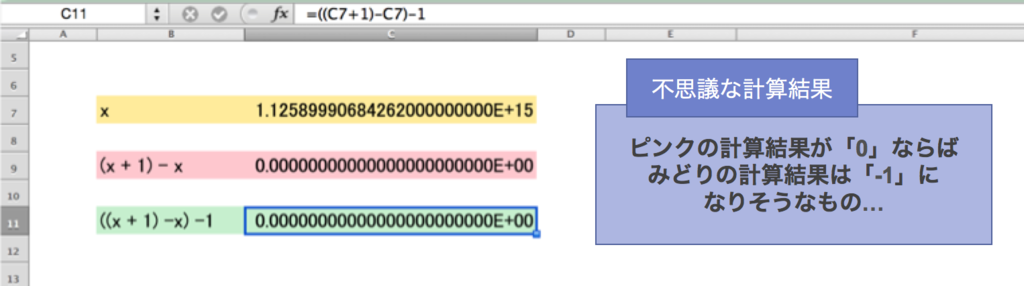
まとめ

CPU を例に浮動小数点環境の精度をあてるプログラムを提示できました。

残念ながら Excel の場合はよくわからない結果になってしまった…。

(Excel が変な挙動を示す新しい例？)

記事が長くなってしまったため、

次回の記事はこのアルゴリズムの証明を紹介予定です。

浮動小数点数については下で詳しくまとめていますので

math-koshimizu.hatenablog.jp

こちらも是非御覧ください！

(追記)

本記事の証明記事書きました！

math-koshimizu.hatenablog.jp

小清水さんとコンピューター数学

コンピューター・数学に関することを書きます (特に丸め誤差の話が多いです。)

計算環境の精度を当てる ― Intel CPU と Excel への応用 ―

Abstract

1. CPU 単精度・倍精度の計算精度を当てる

精度を確かめるプログラムの方針

Step1

Step2

Step3

実際のプログラム

実行結果

2. CPU 拡張倍精度の計算精度を当てる

実行結果

3. Excel の計算精度を当てる!?

と思いますよね？

何がいいたい？

ということはアルゴリズムがおかしい？

まとめ

Abstract

1. CPU 単精度・倍精度 の 計算精度を当てる

精度を確かめるプログラムの方針

Step1

Step2

Step3

実際のプログラム

実行結果

2. CPU 拡張倍精度 の計算精度を当てる

実行結果

3. Excel の計算精度を当てる!?

と思いますよね？

何がいいたい？

ということはアルゴリズムがおかしい？

まとめ

1. CPU 単精度・倍精度の計算精度を当てる

2. CPU 拡張倍精度の計算精度を当てる