小清水 (@curekoshimizu) です。

本日は FMA についてお話したいと思います。

FMA とは？

FMA とは Fused Multiply-Add ことで

$\circ (x\times y + z)$

の演算のことです。ここで $\circ (x)$ は $x \in \mathrm{R}$ の丸めを表しました。

本当にただこれだけの内容なのですが、今回の記事は、この FMA について熱く書いてみたいと思います。

FMA について書くモチベーションなのですが、

本ブログは精度に関する話題を多く取り上げてきました。

その中で FMA と関係する話題が非常に多く登場し、

これからも登場予定です。

そのたびに、 FMA について補足すべきことが多く、ここでまとめておこうと思い立ちました。

例えばこの記事で FMA 命令と丸め誤差の話がすでに登場しています：

math-koshimizu.hatenablog.jp

この記事を読むと

1. FMA の凄さがわかる

精度や高速化と関わることがわかります。

2. 自分の環境で FMA 命令がサポートしているかがわかる

FMA 命令を積んだ HW の歴史についてある程度まとめてみました。

3. サポートがなくとも無理やり FMA 演算を実行する方法がわかる

FMA 命令を積んでいなくとも FMA 計算する方法がありますので紹介します。

4. コンパイルして FMA 命令を出す方法がわかる

FMA 命令をもっていても、実際に使われなくては意味がありません！

5. FMA の応用がわかる

これと関係して、 Horner 法の起源論文なども載せていたりしますので、このあたりに興味ある方も是非ご覧ください。

具体的に何がすごいの？

2つのメリットがあります！

1. 丸め回数が減るので精度的に有利

2. HWサポートがある場合に速度的に有利

すごい点その1 – 丸め回数が減るので精度的に有利

上の $x \times y + z$ を FMA 命令を使わずに計算すると

$\circ \left( \circ (x\times y) + z \right)$

と加算命令1回、乗算命令1回の演算で計算されることになります。

つまり、 2回の丸め が発生します。

それが FMA 命令だと

$\circ (x\times y + z)$

と 1回の丸めしか入らないため、精度的な観点で有利になります。

すごい点その2 – HWサポートがある場合に速度的に有利

この FMA は多くの最新 CPU で FMA 命令を HW サポートしています！

さらに CPU だけでなく GPU などの HW でもサポートしていることが多いです。

これにより

$\circ (x\times y + z)$

という演算を 1回で計算できます。もっていなければ乗算命令と加算命令の 2回で実行する必要があるわけです。 (丸めによる誤差は度外視すると)

これがどういった意味をもつのでしょうか？

この FMA の力をみるべく、 Geforce GTX 1080

という GPU を例に理論ピーク性能を算出してみましょう。

Geforce GTX 1080 の能力は

2560 CUDA コア
1.733 GHz

で動作し、この CUDA コア1つで単精度の FMA 命令を発行できます。

FMA は乗算・加算の 2つの命令分なので 2回の浮動小数点が計算できるという定義になります。

これより単精度理論ピーク性能は

2560 (CUDA コア) $\times$ 1.733 (GHz) $\times$ 2 (FLOPS/(CLOCK $\times$ CUDAコア)) = 8872 GFLOPS

となります。

FMA 命令をもっていないとこの「2」の乗算がなくなりピーク性能指標は、半分になってしまいます。

余談になりますが、この GTX 1080 は単精度で 8.8TFLOPS の力を持っているということで、 2017年現在の GPU はこんなにも能力が高いのか…と思わされます。

このように、性能指標にも活躍するのが FMA 命令です！すなわち、この命令を使わないと事実上、ピーク性能の半分しか理論上だすことができません。

このため、FMA 命令をちゃんと使ってあげることが、 HW の力を引き出しているかどうかと密接な関係があります。

FMA 命令 HW サポートしてる？

ただしこの FMA、多くの CPU でサポートと書きましたが、比較的古い CPU を使っている方はサポートされていない可能性があります。

私のデスクトップ・ノートPC は次のような環境です：

(デスクトップPC)

CPU : Core i7-3820 CPU @3.60GHz
メモリ : 64GB (DDR3-1600)

(ノートPC)

CPU : Core i5-4288U CPU @ 2.60GHz
メモリ : 8GB (DDR3-1600)

こちら、メモリだけでみるとデスクトップの性能がすごくいいです！

しかしながら FMA 命令をサポートしているかどうかでいうと、

ノートPC は FMA命令をサポート しており、デスクトップは 非サポート であります。

そのため、FMA を試す環境としては、私のデスクトップ環境は非常によろしくないです。

このあたりの FMA が載っている載っていないの境界は 2011〜2013 年ごろの CPU にあり、 それについても後述します。

また FMA が載っていなくとも、 FMA の計算、すなわち

$\circ (x\times y + z)$

の計算をできます！

これは HW サポートをしていないのでかなり遅いですが、精度上の恩恵を受けるために使うことができるという意味です。

これについても後述します。

FMA とその歴史

FMA が載っているかどうか怪しいという話を上でしましたが、何時頃登場したのでしょうか？

最初に FMA 命令を積んだのは 1990年の IBM RS/6000 です。

IBM RS/6000 に関する論文「Design of the IBM RISC System/6000 floating-point execution unit」には次のように書かれています：

The IBM RISC System/6000® (RS/6000) floating-point unit (FPU) exemplifies a second-generation RISC CPU architecture and an implementation which greatly increases floating-point performance and accuracy. The key feature of the FPU is a unified floating-point multiply-add-fused unit (MAF) which performs the accumulate operation (A times B) + C as an indivisible operation.

このように、性能と精度を向上するべく搭載されたのが FMA です。この当時、この命令は MAD (multiply-add-fused) と略されていたようです。

その後、浮動小数点の規格として採択されたのは 2008 年のことになります。 IEEE754-2008 に FMA について厳格な仕様が定められました。

その仕様が定まる前にも既に

IBM Power/PowerPC
HP/Intel IA-64
HAL/Fujitsu SPARC64 VI

などで実装されていました。

そのため、2008 年頃にはだいたい CPU は FMA 命令もっているのかな？と思います。

歴史的に気をつけたいのが、我々のデスクトップ環境やノートPCなどで使われている x86_64 、 Intel CPU や AMD CPU です。

対応されたのはまあまあ最近の話だということがわかります。 (最近の感覚がずれていたらすみません)

FMA と Intel CPU

これらは Intel CPU であれば Haswell になって、ようやく FMA サポートしています。

具体的には Intel Core シリーズを最近までの表を下に載せてみますと

第1世代: Nehalem
第2世代: Sandy Bridge
第3世代: Ivy Bridge
第4世代: Haswell (2013年頃)
第5世代: Broadwell
第6世代: Skylake
第7世代: Kaby Lake (2017年現在頃)
第8世代: Coffee Lake

となっており第4世代 Haswell から FMA 命令が HWサポートされました。

(デスクトップPC)

CPU : Core i7-3820 CPU @3.60GHz
メモリ : 64GB (DDR3-1600)

(ノートPC)

CPU : Core i5-4288U CPU @ 2.60GHz
メモリ : 8GB (DDR3-1600)

先ほどの環境の、 「Core i7-3820」 は第2世代 Sandy Bridge (正確には Sandy Bridge-E) であり FMA 命令をもっていません。一方でノートPCに載っていた 「Core i5-4288U」 は第4世代 Haswell のことであります。

FMA と AMD CPU

一方、 AMD CPU であれば AMD FX、Bulldozer から FMA 命令がサポートされており、最近の何かと話題な AMD Zen シリーズの Ryzen もサポート済みです。

このあたりは細かいことを言うと、さらにもう少しややこしく、レジスタをいくつ使うかという点で異なる FMA3・FMA4 のどちらを主流とするかの歴史バトルが Intel・AMD でありました。

FMA3 とは例えば

$x = \circ (x\times y + z)$ $x = \circ (y\times z + x)$

という3レジスタの命令です。一方で FMA4 は

$w = \circ (x\times y + z)$

という4レジスタの命令です。

Intel は FMA3 しか最初からサポートしていませんでしたが、 AMD の最初に FMA サポートした Bulldozer (2011年頃) は FMA4 のみをサポートしていました。

最近登場した Ryzen は FMA4 を非サポートとし、 FMA3 のみをサポート としていますから、

FMA3 のほうが主流となりそうです。

さて、上記のような FMA 命令の中のさらに分類の話はおいておくとして、

結局のところ 2011〜2013年付近の x86_64 頃から、大雑把に FMA 命令が使えるようになってきたということになります。 (具体的には Intel なら Haswell、AMD ならBulldozer)

ここで誤解しないで頂きたいのは、 Intel 初の FMA 搭載 CPU が Haswell というわけではありません。例えば、 Itanium という IA-64 が 2001 年頃にありまして、既に FMA 命令もっていました。

加えて、この年代を超えていたら必ず FMA を持っているというわけではありませんので、自身の CPU を調べてみてください！例えば Linux であれば /proc/cpuinfo の中をみてみるとサポートしているかわかります。

(FMAサポートしている：Core i5-4288Uでの結果)

f:id:curekoshimizu:20170806145146p:plain

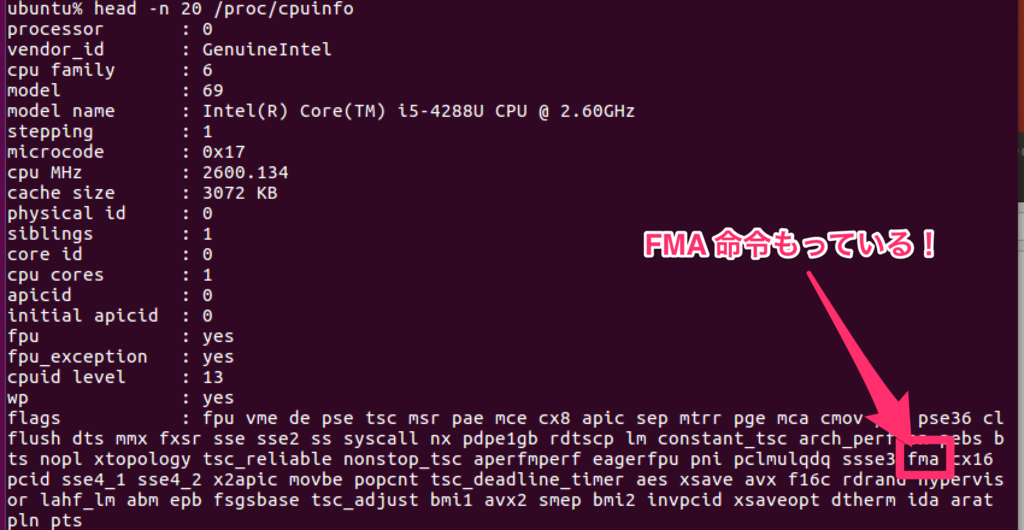
話が脱線気味なので次の話題に移ります。

せっかくFMA命令をもっていても、実際に使われていなければ意味がありません！プログラミング言語・コンパイラの最近の状況はどうなのでしょうか？

FMA とプログラミング言語

C言語・C++言語だけの話に限定しますが、 C言語であれば C99 で FMA 計算用の関数をサポートしており、 C++言語であれば C++11 でサポートしています。

具体的には fmaf・fma・fmal という関数名で提供されています。順に float・double・long double 用 になります。

C99 は名前の通り1999年の規格なわけですが、 FMA 演算

$\circ (x\times y + z)$

を HW サポートしていたのは上でも書いたとおり最近の話になります。

実は HW サポートしていなくとも FMA 計算はできます！

ただしかなりの命令数を使うため HWサポートされていない場合は遅いです！！

あまりにも命令数がかかるため、ここでは「FMA計算」とあえて書きました。

ここに注意してください。

FMA とコンパイラの最適化

例えば FMA を HW サポートしている場合、コンパイラは自動的に FMA 命令に変更してくれたりするのでしょうか？

実はこのあたりが、さらにややこしい話をもたらします。

このあたり gcc と clang で話が少し違うのです。

コンパイラと最適化オプション

gcc も clang も最適化オプションをもっており、デフォルトでは最適化を行わない設定になっています。

gcc・clnag の最適化オプションとして代表的なものは次です：

-O0 (default:最適化なし)
-O1
-O2
-O3
-Ofast

下にいくほどコンパイラにより最適化されます。

参考までに他にも次のような最適化オプションなどがあります：

-Og : Optimize debugging experience
-Os : Optimize for size

それぞれの最適化でどういったことをするかについて調査するには、次を参考にするといいかもしれません：

(gcc)

(clang)

https://stackoverflow.com/questions/15548023/clang-optimization-levels

-march=native オプション

上の最適化オプションだけでは CPU による違いは気にしません。具体的には

先ほどの Intel CPU の

第1世代: Nehalem
第2世代: Sandy Bridge
第3世代: Ivy Bridge
第4世代: Haswell (2013年頃)
第5世代: Broadwell
第6世代: Skylake
第7世代: Kaby Lake (2017年現在頃)
第8世代: Coffee Lake

といった違いは、上の -O系のオプションだけをつけても吸収してくれません。

具体的には上の最適化オプションだけをつけても、 FMA 命令をもつ Haswell と FMA 命令をもたない Sandy Bridge のような CPU のどちらでも動作できるようにするため、

結論としては「FMA命令をもたないコード」が生成されることになります。

高精度・高速度な命令である FMA をもっていても、-O系のオプションをつけるだけでは使われないのです。

非常にもったいないです！

その最適化を支援するために、 この CPU だけでしか使わないよ？ とか、 この演算ができるCPUでしか使わないよ？ と伝えるオプションがあります。

それが例えば -march=native になります。

例えば gcc 5.4.0 を使って Core i7-3820 が乗った環境では

$ gcc -march=native

をつけるとと次のようなオプションが有効になります：

-march=sandybridge -mmmx -mno-3dnow -msse -msse2 -msse3 -mssse3 -mno-sse4a -mcx16 -msahf -mno-movbe -maes -mno-sha -mpclmul -mpopcnt -mno-abm -mno-lwp -mno-fma -mno-fma4 -mno-xop -mno-bmi -mno-bmi2 -mno-tbm -mavx -mno-avx2 -msse4.2 -msse4.1 -mno-lzcnt -mno-rtm -mno-hle -mno-rdrnd -mno-f16c -mno-fsgsbase -mno-rdseed -mno-prfchw -mno-adx -mfxsr -mxsave -mxsaveopt -mno-avx512f -mno-avx512er -mno-avx512cd -mno-avx512pf -mno-prefetchwt1 -mno-clflushopt -mno-xsavec -mno-xsaves -mno-avx512dq -mno-avx512bw -mno-avx512vl -mno-avx512ifma -mno-avx512vbmi -mno-clwb -mno-pcommit -mno-mwaitx --param l1-cache-size=32 --param l1-cache-line-size=64 --param l2-cache-size=10240 -mtune=sandybridge

例えばキャッシュの大きさや SSE命令 (Streaming SIMD Extensions) のどれをサポートしているかなどを、コンパイラに伝えていることがわかります。

ここでわかることは、

-mno-fma
-mno-fma4
-avx512ifma

というオプションがついており、FMA命令をもっていないんだろうな… ということが容易に想像つきます。

-march=native でどういったオプションが有効になるかについては次の記事が参考になります：

http://d.hatena.ne.jp/tmatsuu/20090110/1231557035

また、ここまで紹介した -O1/-O2/-O3/-Ofast や -march=native をつけるとどの程度速くなるかについては、例えば次の記事が参考になるかもしれません：

http://www.phoronix.com/scan.php?page=news_item&px=GCC-Optimizations-E3V5-Levels

このあたりの最適化オプションを勉強するだけでも面白いです。

FMA が発行されるための最適化オプションは？

FMA 命令をもった Haswell 環境で次のコードをコンパイルしてみましょう。

float fma_test(float x, float y, float z)
{
    return x*y + z;
}

$ gcc -S hoge.c

でコンパイルすると次のようになります：

        .....
    mulsd   -16(%rbp), xmm0
    addsd   -24(%rbp), %xmm0
        .....

つまりは FMA命令が使われず乗算と加算命令で実行されることになります。

$ gcc -O3 -march=native

でコンパイルするとどうでしょうか？

        .....
    vfmadd132sd     %xmm1, %xmm2, %xmm0
        .....

と FMA 命令 (詳しくは上で説明したFMA3命令) が発行されていることがわかります。

一方で

$ clang -O3 -march=native

はどうでしょうか？

        .....
    vmulsd  %xmm1, %xmm0, %xmm0
    vaddsd  %xmm2, %xmm0, %xmm0
        .....

と FMA 命令が使われません。

つまり、気をつけたいポイントは gcc・clang のオプションを揃えても FMA 化されるか違う場合があるということです。

この違いを調査した表が次になります：

float fma_test(float x, float y, float z)
{
    return x*y + z;
}

上のコードは次のオプションで FMA命令が呼ばれるかの表

(Core i5-4288U CPU (Haswell/ FMA をもつCPU))

オプション	gcc 5.4.0	clang 3.8.0
-O0	×	×
-O1	×	×
-O2	×	×
-O3	×	×
-Ofast	×	×
-march=native -O0	×	×
-march=native -O1	×	×
-march=native -O2	○	×
-march=native -O3	○	×
-march=native -Ofast	○	○

(Core i7-3820 (Haswell/ FMA をもたないCPU))

オプション	gcc 5.4.0	clang 3.8.0
-O0	×	×
-O1	×	×
-O2	×	×
-O3	×	×
-Ofast	×	×
-march=native -O0	×	×
-march=native -O1	×	×
-march=native -O2	×	×
-march=native -O3	×	×
-march=native -Ofast	×	×

まず march=native の重要性がわかります。これがないと FMA 命令をもたないかもしれませんので FMA 命令は発行されません。

また gcc と clang で FMA が有効になる最適化ポイントが違います。 gcc ならば -O2 から clang なら -Ofast からのようです。

-ffp-contract というオプションがあるのですが、これをつけると clang でも -O1 から可能ならば fma 命令が発行されるようになります。

オプション	gcc 5.4.0	clang 3.8.0
-ffp-contract=fast -march=native -O0	×	×
-ffp-contract=fast -march=native -O1	×	○(変更点)
-ffp-contract=fast -march=native -O2	○	○(変更点)
-ffp-contract=fast -march=native -O3	○	○(変更点)
-ffp-contract=fast -march=native -Ofast	○	○

この -ffp-contract は gcc のリファレンスにこのように記載されています：

-ffp-contract=off disables floating-point expression contraction. -ffp-contract=fast enables floating-point expression contraction such as forming of fused multiply-add operations if the target has native support for them. -ffp-contract=on enables floating-point expression contraction if allowed by the language standard. This is currently not implemented and treated equal to -ffp-contract=off.

The default is -ffp-contract=fast.

これをみると gcc は既に -ffp-contract オプションがついています。一方で clang は挙動が変わったことからもデフォルトが fast になっていないようです。

このあたりにコンパイラの思想の違いがあるように見受けられます。

また、 gcc でも -O1 で最適化してもらうには -fexpensive-optimizations をつけると大丈夫です。

さらに、 -march=native はいくつかのオプションをつけてもらうためのものだったわけですが、実際のところは -mfma が本質的です。

そのためまとめると

float fma_test(float x, float y, float z)
{
    return x*y + z;
}

というコードは

$ gcc   -march=native -O2
$ gcc   -march=native -O1 -fexpensive-optimizations

$ gcc   -mfma         -O2
$ gcc   -mfma         -O1 -fexpensive-optimizations

$ clang -march=native -Ofast
$ clang -march=native -O1 -ffp-contract=fast

$ clang -mfma         -Ofast
$ clang -mfma         -O1 -ffp-contract=fast

のいずれかで FMA 命令に展開されることがわかります。

#include <math.h>

float fma_test(float x, float y, float z)
{
    return fma(x, y, z);
}

としてみましょう。

この場合は

(Core i5-4288U CPU (Haswell/ FMA をもつCPU))

オプション	gcc 5.4.0	clang 3.8.0
-O0	×	×
-O1	×	×
-O2	×	×
-O3	×	×
-Ofast	×	×
-march=native -O0	○	○
-march=native -O1	○	○
-march=native -O2	○	○
-march=native -O3	○	○
-march=native -Ofast	○	○

(Core i7-3820 (Haswell/ FMA をもたないCPU))

オプション	gcc 5.4.0	clang 3.8.0
-O0	×	×
….	….	….
-march=native -Ofast	×	×

となり、HW命令さえもっていれば FMA に展開されます。

そのため、どうしても FMA を発行させたい場合には有効な方法と言えます。

まとめますと

#include <math.h>

float fma_test(float x, float y, float z)
{
    return fma(x, y, z);
}

というコードは

$ gcc   -march=native
$ gcc   -mfma

$ clang -march=native
$ clang -mfma

で展開されます。こちらは -O0 でも大丈夫なところが大きな違いです。

また、 clang であっても -ffp-contract=fast も必要ありません。それは既にユーザーが FMA 演算箇所を指定しているからです。

FMA のハードウェアサポートがない場合に C99 FMA 関数を呼ぶと？

この計算が

$\circ (x\times y + z)$

きちんと発行できます！

ただし、問題は複数命令で実行しているので遅いという点です。

それをみるべく次のことをみてみましょう。

HWサポートがない場合に単精度浮動小数点用の C99 FMA 関数の fmaf を使った実行ファイルを nm コマンドにかけてみますと

$ nm a.out | grep fmaf
                 U fmaf@@GLIBC_2.2.5

となり glibc の fmaf 関数を呼んでいることがわかります。

具体的には glibc のコードの

sysdeps/ieee754/dbl-64/s_fmaf.c

が呼ばれており、ソフトウェアで実装されています。

この実装は次の論文が元になっています：

http://www.lri.fr/~melquion/doc/08-tc.pdf

つまり、高速化という観点ではなく丸めの影響を抑えるため、複数の計算で実現しているというわけです。

これについては丸め誤差の面白い技法が使われており、詳しく紹介してみたいと思っております。

FMA 応用事例 – 多項式計算による FMA の利点

ここまでいろいろ知らないと、 FMA 命令の恩恵が得られないことがわかります。

そして、FMA 命令を使うことなんてそんなにあるの？という声があります。

非常にたくさんあります！

紹介する事例が多すぎるため、

ここでは多項式計算で考えてみたいと思います。

次の多項式を考えてみましょう

$2 {x}^{7} -7 {x}^{6} + 12{x}^{5} - 50{x}^{4} - 2{x}^{3} - 66 {x}^{2} - 60{x} + 54$

こうした例えば 5次の方程式を計算することがあると思いますが、 $a_{k} x^{k}$ という式を $k$ 回の乗算で計算すると 0+1+2+3+4+5+6+7 = 28回の乗算と 7回の加減算で実行することになります。つまり 35 回の丸めが発生します。

これを例えば次のような括弧の付け方で考えます

$2 \left( {x}^{7} -7 \left( {x}^{6} + 12 \left( {x}^{5} -50 \left( {x}^{4} - 2 \left( {x}^{3} - 66 \left( {x}^{2} + ( -60 {x} + 54) \right) \right) \right) \right) \right) \right)$

すると、 $x^{k}$ という式を $(k-1)$ 回の乗算で計算すると 0+0+1+2+3+4+5+6 = 21回の乗算と 7回のFMAで実行することになります。つまり 28 回の丸めが発生します。

つまり 35 回の丸めが入る式から 28 回の丸めが入る式に変わりました。

さらに、上の 5次方程式は次の Horner 法とよばれる形に変換してあげることができます：

$\left( \left( \left( \left( \left( \left( 2{x} -7 \right){x} +12 \right){x} -50 \right) {x} -2 \right) {x} -66 \right) {x} -60 \right) {x} + 54$

こうすると FMA 7 回で計算できてしまいます。

ちなみに Honer法 (ホーナー法) は非常に有名であり、気になり起源論文も調べてみました。 1819年の Honer の論文になります：

http://www.ece.cmu.edu/~ece447/s12/lib/exe/fetch.php?media=wiki:horner-1819.pdf

もちろんこの Honer法は有名なのですが、高速化の観点にたてば、例えばこのような式変形も注目すべきです。

$( {x}^{2} + 5)\left( ( {x}^{2} + 3) \left( ({x}^{2}-2)(2{x}-7)-8 \right) -9 \right) + 9$

この方法にしますと 7回の FMA 演算で計算できてしまいます。

この特徴は並列に計算可能な 4つの FMA 演算が

${x}^2 + 5$
${x}^2 + 3$
${x}^2 - 2$
$2x-7$

登場することであり、この点で Honer 法より有利に働きます。

こうした多項式計算技法はいろいろ知られており、どこかでまとめたいと思っています。

最後に

ここまで FMA についていろいろ紹介してみました。

FMA はかなり役に立つ命令だったり、性能向上に役立つものですので、是非ご活用ください！

また、もし家庭でPCの購入予算がおりない場合、

今のPCはFMAがサポートしてないけど最近のはFMAが載っているから、だいたい2倍くらい性能いいらしいよ！っていえば奥さんも説得できそうな気がします。

そんな時にも使ってみてください。

FMA は丸め誤差の話とすごく関わるため、今後このブログでは頻繁に登場予定です！

よろしくお願いします。

こんなにも数式が出てこなかったのは、この記事が初めてかもしれません。

小清水さんとコンピューター数学

コンピューター・数学に関することを書きます (特に丸め誤差の話が多いです。)

FMA (Fused Multiply-Add) について色んな観点でまとめてみた

FMA とは？

具体的に何がすごいの？

すごい点その1 – 丸め回数が減るので精度的に有利

すごい点その2 – HWサポートがある場合に速度的に有利

FMA 命令 HW サポートしてる？

FMA とその歴史

FMA と Intel CPU

FMA と AMD CPU

FMA とプログラミング言語

FMA とコンパイラの最適化

コンパイラと最適化オプション

-march=native オプション

FMA が発行されるための最適化オプションは？

FMA のハードウェアサポートがない場合に C99 FMA 関数を呼ぶと？

FMA 応用事例 – 多項式計算による FMA の利点

最後に

FMA とは？

具体的に何がすごいの？

すごい点その1 – 丸め回数が減るので精度的に有利

すごい点その2 – HWサポートがある場合に速度的に有利

FMA 命令 HW サポートしてる？

FMA とその歴史

FMA と Intel CPU

FMA と AMD CPU

FMA と プログラミング言語

FMA とコンパイラの最適化

コンパイラと最適化オプション

-march=native オプション

FMA が発行されるための最適化オプションは？

FMA の ハードウェアサポートがない場合に C99 FMA 関数 を呼ぶと？

FMA 応用事例 – 多項式計算による FMA の利点

最後に

FMA とプログラミング言語

FMA のハードウェアサポートがない場合に C99 FMA 関数を呼ぶと？