小清水さんとコンピューター数学

コンピューター・数学 に関することを書きます (特に丸め誤差の話が多いです。)

計算環境の精度を当てる ― 解説編 ―

小清水 です。 (@curekoshimizu)

前回の記事は

「計算環境の精度を当てる ― Intel CPU と Excel への応用 ―」というタイトルで、

\beta 進 p 桁浮動小数点環境 の

基数 \beta と 精度 p を当てる！

という話でした。 (一部 Excel の謎挙動を紹介)

math-koshimizu.hatenablog.jp

前回は証明を掲載していなかったため、

今回は証明に主眼をおいて紹介したいと思います。

最初に注意しますが、

\beta は 2以上の整数 とします。

世の中には 「-2 進数」・「1+i進数」・「黄金進数」などというのがあったりもするのですが、

さすがに除外させてください。

(これらが採用された実用的なコンピューターを僕はまだ知りません。)

証明がわかりやすいよう、

記号 \circ (x) を次で定義しておきます：

\circ (x) の定義
\circ (x) を x について \beta 進 p桁環境 で計算した際の結果
と定義します。
ただし丸めの方向は環境に決っているものとし、
最もよく使われる「最近接偶数方向丸め」でなくとも構いません。

丸めの方向 、例えば、

最もよく使われる 最近接偶数方向丸め や 0方向丸め などについて知りたい方はココを御覧ください：

math-koshimizu.hatenablog.jp

3進数3桁の環境でアルゴリズムを振り返りながら+証明

実例があったほうがわかりやすいかと思いますので、 ありきたりな 2進数 ではなく 3進3桁 で考えましょう。

以前紹介していたように、

Step1・2・3 がありました。

Step のそれぞれのアルゴリズムを思い出し、

次にそれを 3進3桁で実例を動かし、

そのアルゴリズムで結局何を実行しようとしているのかとその証明を述べていこうと思います。

Step1. について

Step 1
x_0 = \circ{(1)} = 1 から始め、
x_{m+1} = \circ{(2\times x_m)} と計算していく。
つまり {2}^{n} を \beta 進 p 桁で計算していくということになります。
そして、初めて \circ{( \circ (x_m + 1) - x_m)} \neq 1 となる x_m を求めます。

実例でみていきましょう。

Step1 を実例で考える

{2}^{0} = 1 の 3進3桁表現は {(1.00)}_{3} \times {3}^{0} です。

{2}^{1} = 2 の 3進3桁表現は {(2.00)}_{3} \times {3}^{0} です。

これを続けていくと、

f:id:curekoshimizu:20170129201119p:plain

となります。注意としては {(1.21)}_{3} \times {3}^{2} の次 ( \times 2) は

本来は {(1.012)}_{3} \times {3}^{3} なのですが、

これは 4桁精度 の表現なので、

3桁精度 に丸める必要があります。

このアルゴリズムは 丸めの方向に言及していない ことから、

近い2つの浮動小数点のどちらを選んでも問題ありません！

つまり候補としては 2つ あり、この例ですと

\circ ({(1.012)}_{3} \times {3}^{3}) = {(1.01)}_{3} \times {3}^{3} または {(1.02)}_{3} \times {3}^{3}

となります。

f:id:curekoshimizu:20170130000236p:plain

ここまで登場した、オレンジ以外の数 を x としても

(x + 1) - x の計算値は 1 になります。

例えば、ピンクの数である、

x = {(1.21)}_{3} \times {3}^{2} で詳しくみてみましょう。

x + 1 = {(1.21)} \times {3}^{2} + {(1.00)} \times {3}^{0}

ここで 桁あわせを行い

= {(1.21)} \times {3}^{2} + {(0.01)} \times {3}^{2}

= {(1.22)} \times {3}^{2}

と途中で丸めなのも必要なく、

x+1 を正確に表すことができています。

しかしながら、オレンジの 指数3 の数はこうはなりません。

例えば {(1.12)}_{3} \times {3}^{3} を選択した場合を例にあげると

f:id:curekoshimizu:20170130000335p:plain

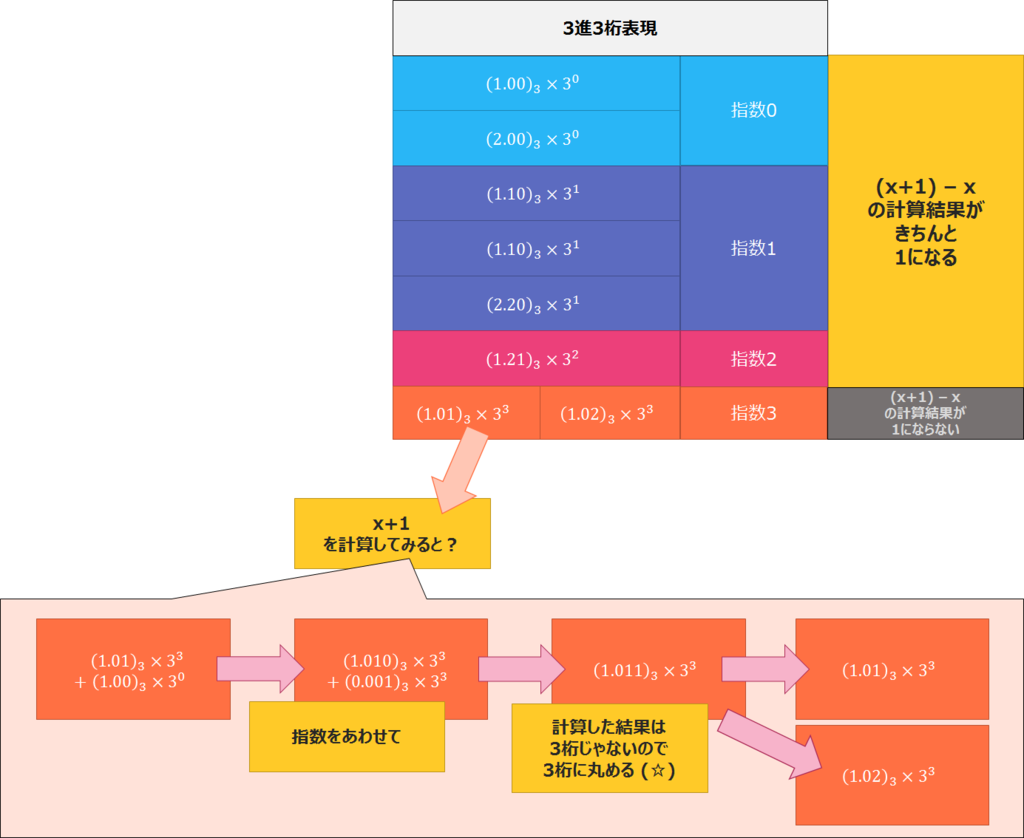
ここでわかるのは 1 の効果が丸めによって(☆)、復元不能になっていることです。

最終結果は丸めの方向によって、

  • {(1.20)}_{3} \times {3}^{3}
  • {(1.12)}_{3} \times {3}^{3}

の2つがでていますが、もとの x = {(1.12)}_{3} \times {3}^{3} から見ると

差が 3 または 0 となっています。

すなわち、 1 という 指数0 の項の影響が、 指数1 の世界に持ち上がってしまったというイメージです。

(x + 1) が正しく求められれば、 (x + 1) - x は当然 1になるのですが、

(x + 1) が真の解からずれてしまうと、もはや (x + 1) - x で 1 に復元することはできなくなります。

すなわち、 Step 1 からわかることは

3進3桁では x_5 = {(1.12)}_{3} \times {3}^{3} で計算が合わなくなるということです。

ここからわかるアルゴリズムの目的と証明

Step1 のアルゴリズム：

Step 1
x_0 = \circ{(1)} = 1 から始め、
x_{m+1} = \circ{(2\times x_m)} と計算していく。
つまり {2}^{n} を \beta 進 p 桁で計算していくということになります。
そして、初めて \circ{( \circ (x_m + 1) - x_m)} \neq 1 となる x_m を求めます。

は何を求めるための Step になるのでしょうか。

\beta 進 p 桁表現の環境における、指数 p表現に属する数 x_m を求めるためのアルゴリズム

実はこれが主張になります。

先程の例でいうと、

f:id:curekoshimizu:20170130000335p:plain

  • 水色 (指数0型)
  • 紫色 (指数1型)
  • ピンク色 (指数2型)

を経て、

  • オレンジ色 (指数3型)

でちょうど Step1 が停止したのです。

この点を一般の場合でも証明しましょう。

Prop 1
整数 m が m < {\beta}^{p} を満たすならば、 m は \beta 進 p 桁で丸め誤差なく表現できる

(証明)

m < {\beta}^{p} なので 0 \leq x_m < \beta なる自然数を使って

\begin{align*} m = x_{p-1} {\beta}^{p-1} + x_{p-2} {\beta}^{p-2} + \dotsb + x_{0} {\beta}^{0} \end{align*}

と表現できる。

ここで x_i \neq 0 となる最大の添字を k とすれば

\begin{align*} m = x_{k} {\beta}^{k} + x_{k- 1} {\beta}^{k- 1} + \dotsb + x_{0} {\beta}^{0} = (x_{k} . x_{k- 1} \dotsb x_0) \times {\beta}^{k} \end{align*}

□

この Prop 1 から {\beta}^{p} を超えない限り {2}^{n} は \beta 進 p桁 で丸め誤差なく表現できる。

{2}^{n} < {\beta}^{p} であるから {2}^{n} + 1 \leq {\beta}^{p} である。

{2}^{n} + 1 < {\beta}^{p} の場合は Prop1 から \beta 進 p桁 で表現可能。

そうでない場合は {2}^{n} + 1 = {\beta}^{p} であり

{\beta}^{p} は = {(1.00\dotsb 0)} \times {\beta}^{p} と表されるので、 \beta 進 p桁 で表現可能。

よって

{2}^{n} < {\beta}^{p} を満たす限り (x + 1) は \beta 進 p桁 で正確に表現可能であるから、

\circ (x +1) = x + 1

となり、

ここから \circ (\circ (x + 1) -x) = \circ( (x +1) -x ) = \circ (1) = 1

ということがわかった。つまり、

Prop 2
Step1 で求める x_n は x_n < {\beta}^{p} を満たす限り x_n = {2}^{n} となり、さらに \circ (\circ (x + 1) -x) = 1 を満たす

ということがわかったことになる。

また、

Prop 3
{\beta}^{p} \leq {2}^{n} < {\beta}^{p+1} を満たす最小の自然数 N がとれる

(証明)

この式を変形すると p\log_2{\beta} \leq {n} < (p+1)\log_2{\beta} であり

この区間の端点間の差は

(p+1)\log_2{\beta} - p\log_2{\beta} = \log_2{\beta} \geq 1

と 1以上のため、区間 \Big[p\log_2{\beta} , (p+1)\log_2{\beta} \Big) には必ず自然数が含まれる。

その自然数が存在し、その最小なものが証明する N である。

□

この Prop3 より 自然数 m として

{\beta}^{p} \leq {2}^{m} < {\beta}^{p+1} を満たし {2}^{m-1} < {\beta}^{p} となるものがとれる。

この式から

\circ ({\beta}^{p}) \leq \circ (2\times {2}^{m-1}) < \circ ( {\beta}^{p+1}) となり、

{2}^{m-1} < {\beta}^{p} であることから Prop 2から x_{m-1} = {2}^{m-1} となる。

すなわち x_m = \circ (2\times x_{m-1}) = \circ ( 2 \times {2}^{m-1} ) であり

{\beta}^{p} \leq x_m < {\beta}^{p+1} を得る。

\circ (x_m + 1) = x_m + \beta , x_m である（両者は {\beta} 進 p 桁で表現可能な x_N + 1 の両端点である。

以上から

Prop 4
{\beta}^{p} \leq x_{m} < {\beta}^{p+1} となり x_{m-1} < {\beta}^{p} となる 自然数 m が存在し、 \circ ( \circ (x_m + 1) - x_m = \beta , 0 を満たす。

ということが示された。

以上から Step1 のアルゴリズムが

\beta 進 p 桁表現の環境における、指数 p表現に属する数 x_m を求めるためのアルゴリズム

となることは Prop2 と Prop4 から示されたことになります。

Step2. について

Step 2
Step1 で求めた {x}_{m} は \circ ( \circ ( x_m + 1) - x_m) \neq 1
であり、この 1 を動かして
\circ ( \circ ( x_m + 2) - x_m) \neq 2
\circ ( \circ ( x_m + 3) - x_m) \neq 3
と続き、 初めて等号となってしまう 整数 \beta を見つる
つまり、
\circ ( \circ ( x_m + \beta) - x_m) = \beta
となる \beta を見つける。

この Step2 から \beta が見つかると

その環境が \beta 進数計算環境であることがわかる

Step2 を実例で考える

先程の 3進3桁 では Step1 により x_5 = {(1.12)}_{3} \times {3}^{3} が求まりました。

\circ ( \circ ({(1.12)} \times {3}^{3} + 1) - {(1.12)} \times {3}^{3}) が 1 にならないことがわかりました。

今度は

\circ ( \circ ({(1.12)} \times {3}^{3} + 2) - {(1.12)} \times {3}^{3})

や

\circ ( \circ ({(1.12)} \times {3}^{3} + 3) - {(1.12)} \times {3}^{3})

を計算していこうという話になります。

計算してみるとわかるのですが下のようになります：

  • \circ ( \circ ({(1.12)} \times {3}^{3} + 1) - {(1.12)} \times {3}^{3}) \neq 1 (Step1)

  • \circ ( \circ ({(1.12)} \times {3}^{3} + 2) - {(1.12)} \times {3}^{3}) \neq 2

  • \circ ( \circ ({(1.12)} \times {3}^{3} + 3) - {(1.12)} \times {3}^{3}) = 3

これは

3 が 3進3桁で {(1.000)}_{3} \times {3}^{1} と 指数1 に初めてなる！

ことが関係します。それまでの数は 指数0 型の表現でした。

さきほど成立しなかった理由を思い出すと、

指数0 の数を足しても、桁数をあわせて足しても 3桁でおさまらないため、

丸める必要がありました。

今回は 指数1 なので、桁をあわせて足した数が 3桁でおさまります。

(x+1) がきちんと表現できてしまえばこちらのものです。

以上から、 3 が求められ、

3進3桁の 3進数 が求められます。

ここからわかるアルゴリズムの目的と証明

目的は上でも記載したとおり、基数 \beta を求めることです。

Step1. で x_m であり

{\beta}^{p} \leq x_m < {\beta}^{p+1}

となるものが得られました。

この数と 1, 2, \dotsb , \beta - 1 の足し算は \beta 進 p 桁で正確に表現できないが、

\beta は (1.000\dotsb ) \times {\beta}^{1} であるから x_m + \beta は正確に表現可能。

よって \circ ( \circ ( x_m + \beta) - x_m ) = \circ ( x_m + \beta - x_m) = \beta となり Step2 で \beta が求まる。

Step3. について

Step3

Step 3
Step2 でわかった \beta を使って y_0 = \circ{(1)} = 1 から始め、
y_{n+1} = \circ{(\beta \times x_n)} と計算していく。
そして、初めて \circ ( \circ ( y_p + 1) - y_p) \neq 1 となる p を求めます。

この p が 精度 p 桁 を表すという主張です。

Step3 を実例で考える + 証明

27 = {(1.000)}_{3} \times {3}^{3} のとき、

初めて (27 + 1) - 27 の計算が 1 に一致しなくなります。

f:id:curekoshimizu:20170129212915p:plain

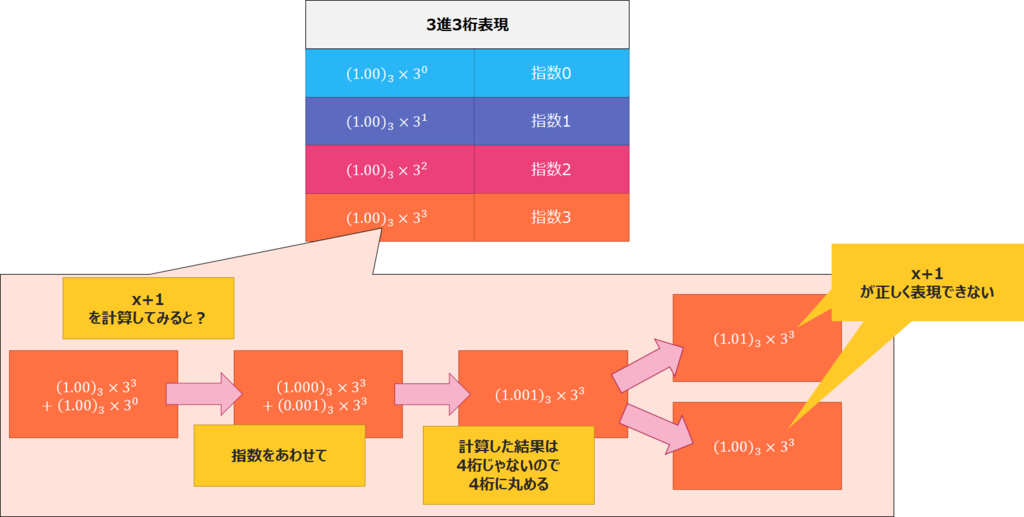
これは Step1 と同じ話で、

何が違うかというと、

Step1 は基数が不明だったので、 {2}^{p} という形でもって調べる必要がありましたが、

今度は {\beta}^{p} 型なので、第 p 回で 指数 p 型になることがわかります。

これが証明であります。

あとは Step1 と同じです。

最後に： \beta が 素数じゃない場合でも？

基数 \beta が素数じゃなくとも、きちんと求まります！

これは Step2 の証明を思い出すとわかります。

ということは

16進法 でもこの基数を当てられる！ということになります。

16 進法といえば 古典的 RISC アーキテクチャである (1970年頃)、

IBM System/370 などに採用されている IBM浮動小数点方式 では

「16進数」を採用していました。

「16進数」は一時期はコンピューターの歴史を彩っていた方式であり、

これを使う機会があれば、

「16進数」である証拠をこのアルゴリズムで確認できます！

以上1万字を超える、浮動小数点を含んだ証明の話でした。

前回の「計算環境の精度を当てる ― Intel CPU と Excel への応用 ―」という記事では、

math-koshimizu.hatenablog.jp

Excel の謎挙動 を紹介しました。これについては現在も調査中です。

大まかにわかってきたのですが、まとまりましたら紹介したいと思っております！

よろしくお願いします。